Importation des données

Les données simulées sont disponibles à même le package. D’autres packages doivent aussi être importés.

library(xgbmr)
library(tidyverse)
#> ── Attaching packages ───────────────────────────────────────────────────── tidyverse 1.3.0 ──
#> ✔ ggplot2 3.2.1     ✔ purrr   0.3.3
#> ✔ tibble  2.1.3     ✔ dplyr   0.8.3
#> ✔ tidyr   1.0.0     ✔ stringr 1.4.0
#> ✔ readr   1.3.1     ✔ forcats 0.4.0
#> ── Conflicts ──────────────────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
library(xgboost)
#> 
#> Attaching package: 'xgboost'
#> The following object is masked from 'package:dplyr':
#> 
#>     slice
library(mlr)
#> Loading required package: ParamHelpers
library(iml)
library(xtable) # pour des fins de présentation
library(gridExtra)
#> 
#> Attaching package: 'gridExtra'
#> The following object is masked from 'package:dplyr':
#> 
#>     combine
dt <- SimulatedIndClaims

Manipulation des données

Avant de pouvoir utiliser les données dans l’algorithme XGBoost, on doit d’abord effectuer un certain traitement des données.

Censuration des données

Dans la pratique, nous ne connaissons pas encore le vrai montant à l’ultime pour les réclamations qui sont plus récentes. Cet aspect a été tenu en compte, et une fonction du package permet de censurer les réclamations pour lesquelles nous ne sommes pas censé connaître l’information

dat <- dt %>% censoreDataset(evalYr = 2005)

set.seed(20191024) # Même seed que dans presentation-data.Rnw
dat %>% 
    select(ClNr, AY, starts_with('Pay'), real_ultimate) %>% 
    sample_n(5) %>% 
  knitr::kable()

ClNr	AY	Pay00	Pay01	Pay02	Pay03	Pay04	Pay05	Pay06	Pay07	Pay08	Pay09	Pay10	Pay11	real_ultimate
10031	1997	0	345	0	0	0	0	0	0	0	NA	NA	NA	345
26457	2002	1015	0	0	0	NA	NA	NA	NA	NA	NA	NA	NA	1015
36641	2005	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0
5903	1995	542	0	0	0	0	0	0	0	0	0	0	NA	542
15129	1999	200	0	0	0	0	0	0	NA	NA	NA	NA	NA	200

Modèle C : estimation des LDF

set.seed(20191023)
index <- makeResampleInstance(
    desc = makeResampleDesc('Holdout', stratify.cols = 'AY', split = 0.70), 
    # il faut absolument donner une tâche et un target bidon
    task = makeRegrTask(data = dt, target = 'Pay00') 
)
traindt <- dat[index$train.inds[[1]],]
testdt <- dat[index$test.inds[[1]],]

mack_bs_tri <- traindt %>% 
    getAggrTriangle() %>% 
    ChainLadder::BootChainLadder(R = 1000)
#> 
#> Welcome to ChainLadder version 0.2.10
#> 
#> Type vignette('ChainLadder', package='ChainLadder') to access
#> the overall package documentation.
#> 
#> See demo(package='ChainLadder') for a list of demos.
#> 
#> More information is available on the ChainLadder project web-site:
#> https://github.com/mages/ChainLadder
#> 
#> To suppress this message use:
#> suppressPackageStartupMessages(library(ChainLadder))

ldf_bs <- mack_bs_tri$simClaims %>% 
    apply(3, function(triangle){
        triangle %>% incr2cum() %>% as.triangle() %>% getLDF()
    }) %>% t() %>% apply(2, quantile, probs = 0.8)

data.frame(LDF = ldf_bs) %>% t() %>% knitr::kable()

	1	2	3	4	5	6	7	8	9	10	11	12
LDF	2.0875	1.3137	1.1673	1.1081	1.07792	1.0533	1.0376	1.0252	1.0168	1.0121	1.0066	1

Préparer les jeux de données

train_a <- traindt %>%
    widetolong() %>%
    filter(complete.cases(.)) %>% # garder les années connues
    filter(!(Open == 1 & Paid == 0)) %>% # enlever masse à 0
    select(-AY, -TotalPaid, -Pay, -still, -max_dev_yr) %>% 
    rename(Ultimate = real_ultimate) %>% 
    # Arranger le dataset final pour le modèle A
    select(ClNr:RepDel, devYear, Paid, Open, Ultimate) %>% 
    as_tibble() 

train_b <- traindt %>% 
    widetolong() %>%
    filter(complete.cases(.)) %>%
    mutate(Ultimate = TotalPaid) %>% 
    filter(!(Open == 1 & Paid == 0)) %>% # enlever masse à 0
    filter(Open == 0) %>% 
    select(-AY, -TotalPaid, -Pay, -still, -max_dev_yr, -real_ultimate) %>% 
    as_tibble()

train_c <- traindt %>%
    widetolong() %>%
    filter(complete.cases(.)) %>% # garder les années connues
    mutate(Ultimate = case_when(
        still == 1 ~ TotalPaid * ldf_bs[max_dev_yr + 1],
        TRUE ~ TotalPaid)) %>% 
    filter(!(Open == 1 & Paid == 0)) %>% # enlever masse à 0
    select(-AY, -TotalPaid, -Pay, -still, -max_dev_yr, -real_ultimate) %>% 
    as_tibble() # pour enlever le tag grouped df

Idem pour le test set :

test <- testdt %>% 
    widetolong() %>%
    filter(complete.cases(.)) %>% # garder les années connues
    rename(Ultimate = real_ultimate) %>% 
    # Arranger le dataset final pour le modèle A
    select(ClNr:RepDel, devYear, Paid, Open, Ultimate) %>% 
    as_tibble()

Entrainement

Étant donné que les modèles xgboost peuvent être long à rouler, des modèles déjà entrainés sur les données d’exemple sont inclus avec le package. Les hyperparamètres des modèles sont disponibles dans la table suivante :

fit_a$learner$par.vals  %>% data.frame(Modèle = 'A', .) %>% 
    bind_rows(fit_b$learner$par.vals  %>% data.frame(Modèle = 'B', .),
              fit_c$learner$par.vals  %>% data.frame(Modèle = 'C', .)) %>% 
  knitr::kable()
#> Warning in bind_rows_(x, .id): Unequal factor levels: coercing to character
#> Warning in bind_rows_(x, .id): binding character and factor vector, coercing
#> into character vector

#> Warning in bind_rows_(x, .id): binding character and factor vector, coercing
#> into character vector

#> Warning in bind_rows_(x, .id): binding character and factor vector, coercing
#> into character vector

Modèle	nrounds	objective	eval_metric	eta	max_depth	min_child_weight	subsample	colsample_bytree
A	1184	reg:squarederror	rmse	0.1	3	20	0.5	0.5
B	66	reg:squarederror	rmse	0.1	3	20	0.5	0.5
C	740	reg:squarederror	rmse	0.1	3	20	0.5	0.5

Note : la vignette entrainement_modeles permet d’avoir un peu plus de détail sur la procédure.

Résultats

test_dt <- test %>% select(-ClNr)
test_tsk <- makeRegrTask(data = test_dt, target = 'Ultimate')
#> Warning in makeTask(type = type, data = data, weights = weights, blocking =
#> blocking, : Provided data is not a pure data.frame but from class tbl_df, hence
#> it will be converted.

Les modèles sont déjà inclus dans le package pour l’exemple

pred_a <- predict(fit_a, test_tsk)
pred_b <- predict(fit_b, test_tsk)
pred_c <- predict(fit_c, test_tsk)

Mettre ensemble les variables explicatives et les prédictions

test_pred_a <- test_dt %>% 
    rownames_to_column('id') %>% 
    mutate_at(vars(id), as.integer) %>% 
    left_join(pred_a$data, by = "id")
test_pred_b <- test_dt %>% 
    rownames_to_column('id') %>% 
    mutate_at(vars(id), as.integer) %>% 
    left_join(pred_b$data, by = "id")
test_pred_c <- test_dt %>% 
    rownames_to_column('id') %>% 
    mutate_at(vars(id), as.integer) %>% 
    left_join(pred_c$data, by = "id")

Distribution prédictive des réserves totales (Bootstrap)

## Vraie réserve (selon données simulées du test set)
vraie_reserve <- test_dt %>% summarise(paye = sum(Paid), total = sum(Ultimate), R = total - paye)

## Calcul des réserves totales selon chaque modèle
aa <- apply(bs_pred_a, 2, sum)
bs_res_a <- (aa - sum(test_dt$Paid)) %>% data.frame(A = .)

bb <- apply(bs_pred_b, 2, sum)
bs_res_b <- (bb - sum(test_dt$Paid)) %>% data.frame(B = .)

cc <- apply(bs_pred_c, 2, sum)
bs_res_c <- (cc - sum(test_dt$Paid)) %>% data.frame(C = .)

Et on obtient le tableau suivant :

bind_cols(bs_res_a, bs_res_b, bs_res_c) %>% 
    gather('Modèle', 'Réserve') %>% 
    group_by(Modèle) %>% 
    nest() %>% 
    mutate(
        moyenne = map_dbl(data,function(x) unlist(x) %>%  mean),
        sd = map_dbl(data,function(x) unlist(x) %>%  sd),
        VaR95 = map_dbl(data,function(x) unlist(x) %>%  quantile(., probs = .95)),
        VaR99 = map_dbl(data,function(x) unlist(x) %>%  quantile(., probs = .99))
    ) %>% 
    select(-data) %>% 
    data.frame() %>% 
    format(big.mark = ' ', justify = 'centre') %>% 
  knitr::kable()

Modèle	moyenne	sd	VaR95	VaR99
A	25 482 234	1 720 920	27 927 106	27 951 939
B	2 937 217	1 653 261	5 326 843	5 885 246
C	24 057 011	1 098 914	25 779 615	26 007 870

Et le graphique suivant :

bind_cols(bs_res_a, bs_res_b, bs_res_c) %>% 
    ggplot() + 
    geom_density(aes(x = A, y = ..density..,  fill = 'A'), n = 2^12, alpha = 0.4) + 
    geom_density(aes(x = B, y = ..density.., fill = 'B'), n = 2^12, alpha = 0.4) + 
    geom_density(aes(x = C, y = ..density.., fill = 'C'), n = 2^12, alpha = 0.4) + 
    theme_classic() + 
    theme(legend.position = 'bottom') + 
    labs(fill = 'Modèles', x = 'Réserve totale', y = 'Probabilité') + 
    geom_vline(xintercept = vraie_reserve$R, linetype = 'dashed')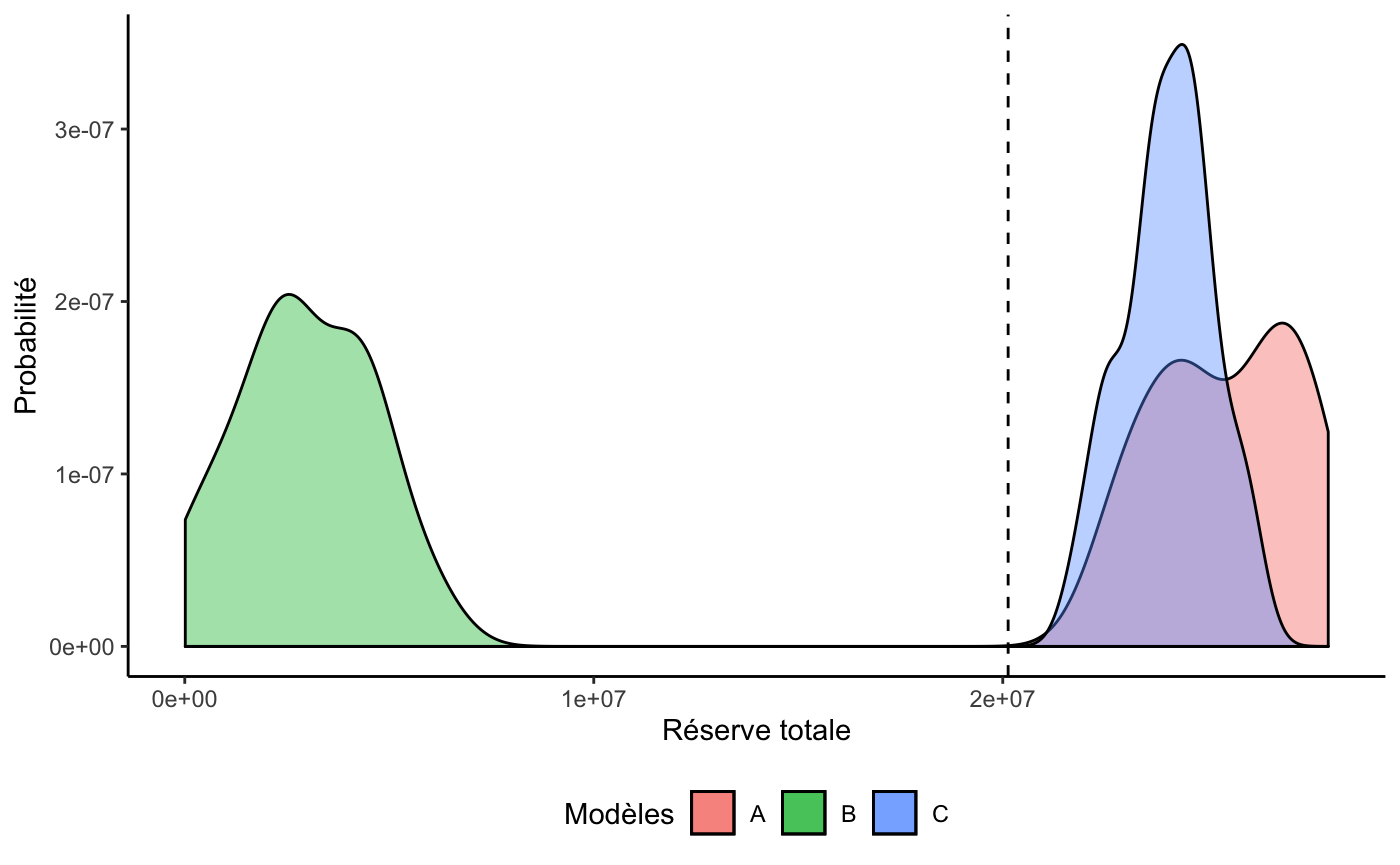

Graphique des prédictions en fonction de la vraie valeur

zoom_out_pred <- pred_c$data %>% 
    # filter(response > 0) %>% 
    ggplot(aes(x = truth, y = response)) + 
    geom_point() + 
    annotate('rect',
             xmin = 0, xmax = 200000,
             ymin = 0, ymax = 200000,
             alpha = 0.3, col = 'blue') +
    # geom_vline(xintercept = qq, col = 'red', linetype = 'dashed') + 
    geom_abline(intercept = 0, slope = 1, 
                col = 'blue', size = 1, linetype = 'dashed') + 
    # coord_cartesian(xlim = c(0, 25000), ylim = c(0,25000)) + 
    labs(y = 'Valeur prédite')

zoom_in_pred <- pred_c$data %>% 
    # filter(response > 0) %>% 
    ggplot(aes(x = truth, y = response)) + 
    geom_point() + 
    # geom_vline(xintercept = qq, col = 'red', linetype = 'dashed') + 
    geom_abline(intercept = 0, slope = 1, 
                col = 'blue', size = 1, linetype = 'dashed') + 
    coord_cartesian(xlim = c(0, 200000), ylim = c(0,200000)) + 
    labs(y = 'Valeur prédite')
zoom <- arrangeGrob(zoom_out_pred, zoom_in_pred)
plot(zoom)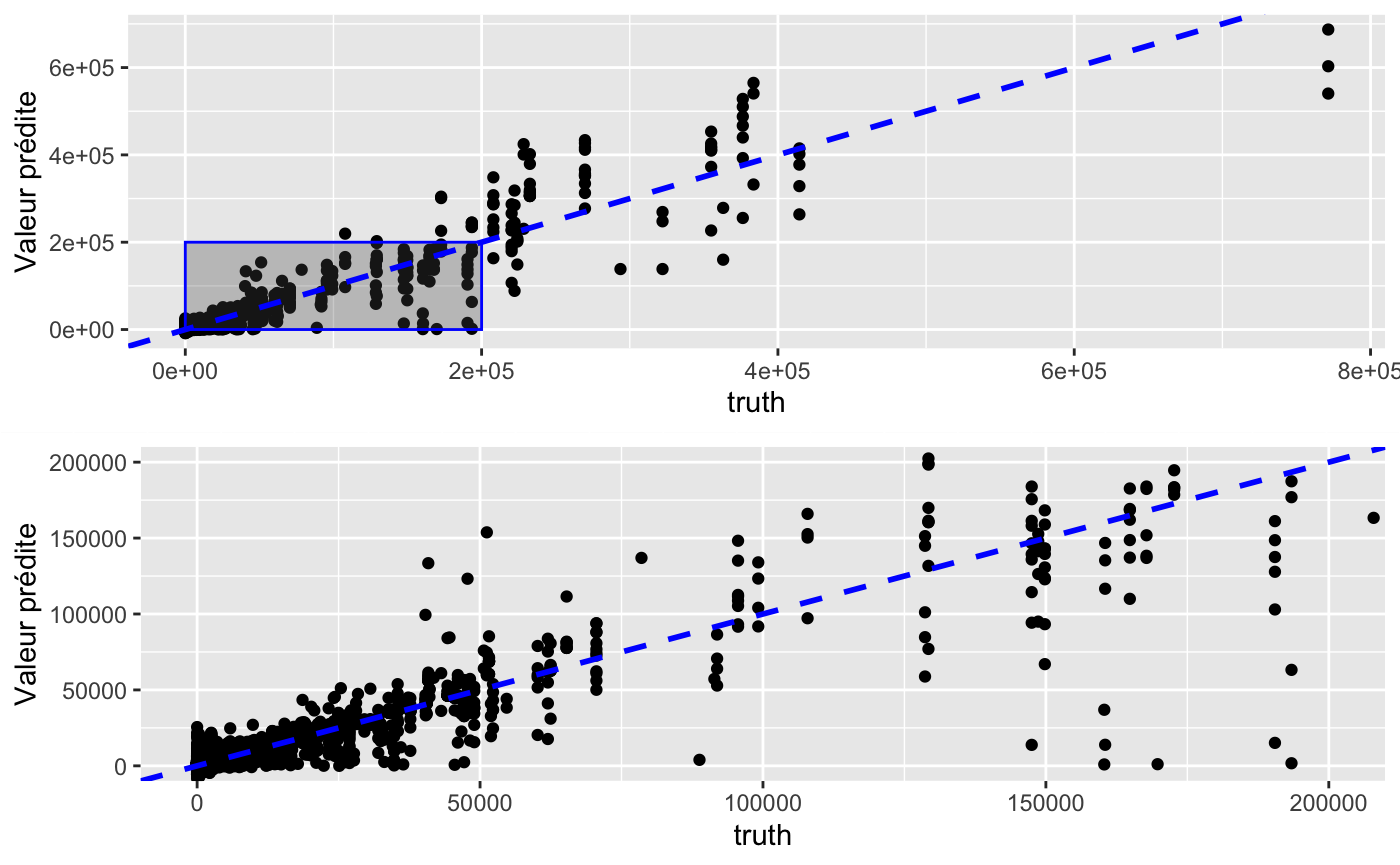

Prediction Lift

pred_a$data %>% 
    rename(A = response) %>% 
    mutate(
        B = pred_b$data$response,
        C = pred_c$data$response
    ) %>% 
    gather('Modèle', 'response', A,B,C) %>% 
    group_by(Modèle) %>% nest() %>% 
    mutate(quantile = map(data, function(dt){
        dt %>% 
            transmute(quantile = ntile(response, n = 5))
    })) %>% 
    unnest(cols = c(data, quantile)) %>% select(-id) %>% 
    group_by(Modèle, quantile) %>% 
    summarise(
        reel_moyen = mean(truth),
        rmse_moyen = sqrt(mean((truth - response)^2))
    ) %>% 
    mutate(quantile = case_when(
        quantile == 1 ~ "(0, 20)",
        quantile == 2 ~ "(20, 40)",
        quantile == 3 ~ "(40, 60)",
        quantile == 4 ~ "(60, 80)",
        quantile == 5 ~ "(80, 100)"
    )) %>% 
    ggplot(aes(x = quantile)) + 
    geom_bar(aes(y = reel_moyen),stat = 'identity', fill = 'green',
             alpha = 0.4, col = 'black') + 
    geom_line(aes(y = rmse_moyen, col = 'RMSE moyen par quantile'),
              linetype = 'dashed', group  =1) + 
    geom_point(aes(y = rmse_moyen), col = 'red') + 
    theme(legend.position = 'bottom', 
          axis.text = element_text(angle = 90, hjust = 1, vjust = 0.5)) +
    coord_cartesian(ylim = c(0, 15000)) +
    labs(
        y = "Valeur réelle moyenne",
        x = "Regroupement des quantiles de la variable réponse", col = NULL) + 
    facet_grid(. ~ Modèle)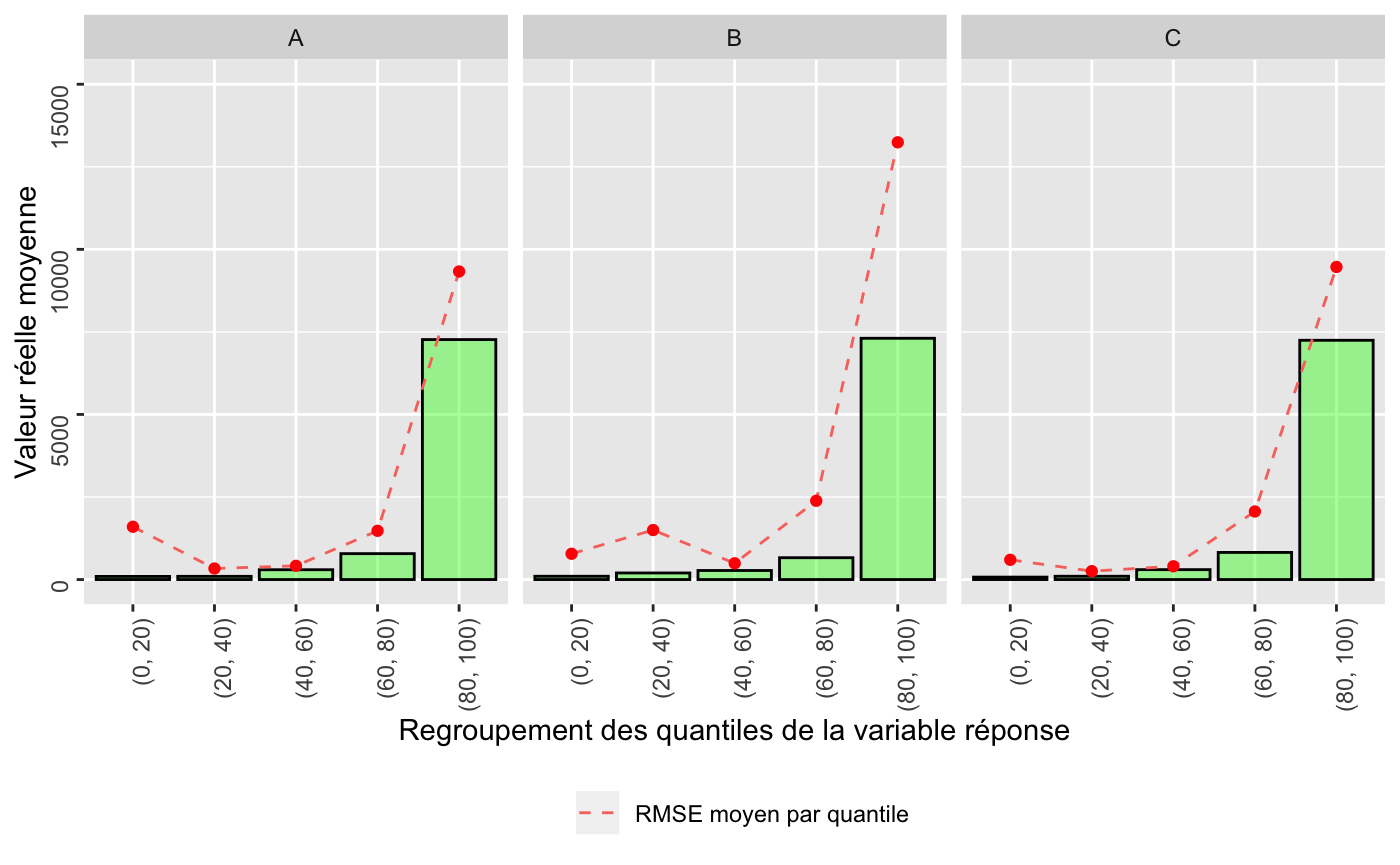

RMSE selon devYear

rmse_selon_variable(test_pred_c, devYear) + 
    scale_x_discrete(limits = 0:11)

Graphique des résidus du modèle C

set.seed(2019)
pred_a$data %>% 
    sample_frac(.1) %>% 
    mutate(erreur = truth - response) %>% 
    ggplot() + 
    geom_histogram(aes(x = erreur), binwidth = 100) + 
    coord_cartesian(xlim = c(-2000, 2000)) + 
    labs(x = expression(epsilon = y[i] - hat(y)[i]),
         y = 'Fréquence',
         caption = 'Échantillon aléatoire de 10% des prédictions sur les données de validation') + 
    scale_y_discrete(limits = seq(0, 2000, 100))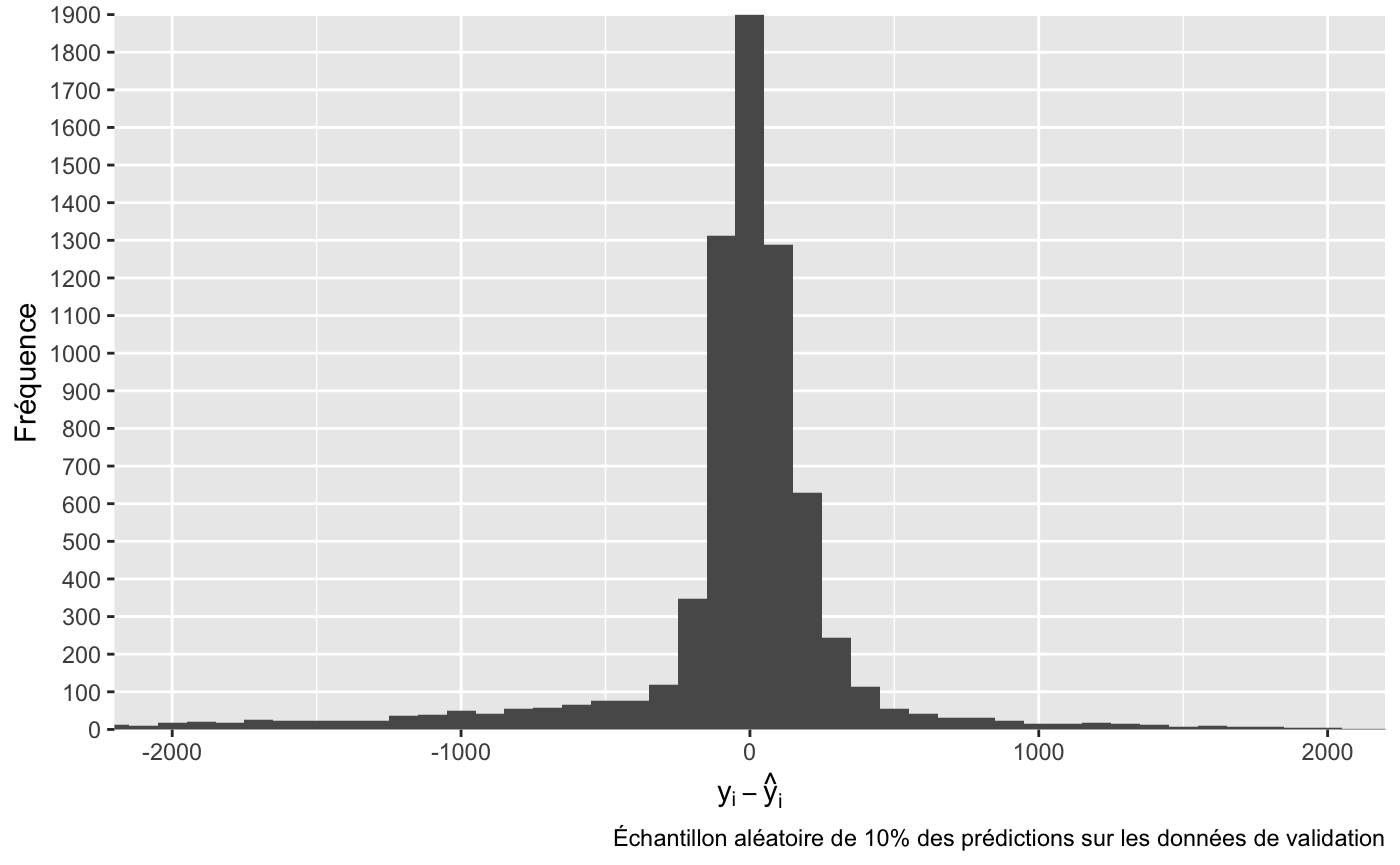

Interptétabilité des modèles

set.seed(2019)
predictor_a <- test_dt %>%
    # On sélectionne 30 observations par année de développement
    group_by(devYear) %>% sample_n(30) %>%
    # on rammène en tibble car iml n'accepte pas un 'grouped_df' de dplyr
    as_tibble() %>% 
    Predictor$new(model = fit_a, data = select(., -Ultimate), y= select(., Ultimate))
predictor_b <- test_dt %>%
    # On sélectionne 30 observations par année de développement
    group_by(devYear) %>% sample_n(30) %>%
    # on rammène en tibble car iml n'accepte pas un 'grouped_df' de dplyr
    as_tibble() %>% 
    Predictor$new(model = fit_b, data = select(., -Ultimate), y= select(., Ultimate))
predictor_c <- test_dt %>%
    # On sélectionne 30 observations par année de développement
    group_by(devYear) %>% sample_n(30) %>%
    # on rammène en tibble car iml n'accepte pas un 'grouped_df' de dplyr
    as_tibble() %>% 
    Predictor$new(model = fit_a, data = select(., -Ultimate), y= select(., Ultimate))

Graphique des Feature importance

varimp_a <- FeatureImp$new(predictor_a, loss = "mse") %>% plot() + theme_classic()
varimp_b <- FeatureImp$new(predictor_b, loss = "mse") %>% plot() + theme_classic()
varimp_c <- FeatureImp$new(predictor_c, loss = "mse") %>% plot() + theme_classic()
# grid.arrange(varimp_a, varimp_b, varimp_c, nrow = 3)
varimp_c

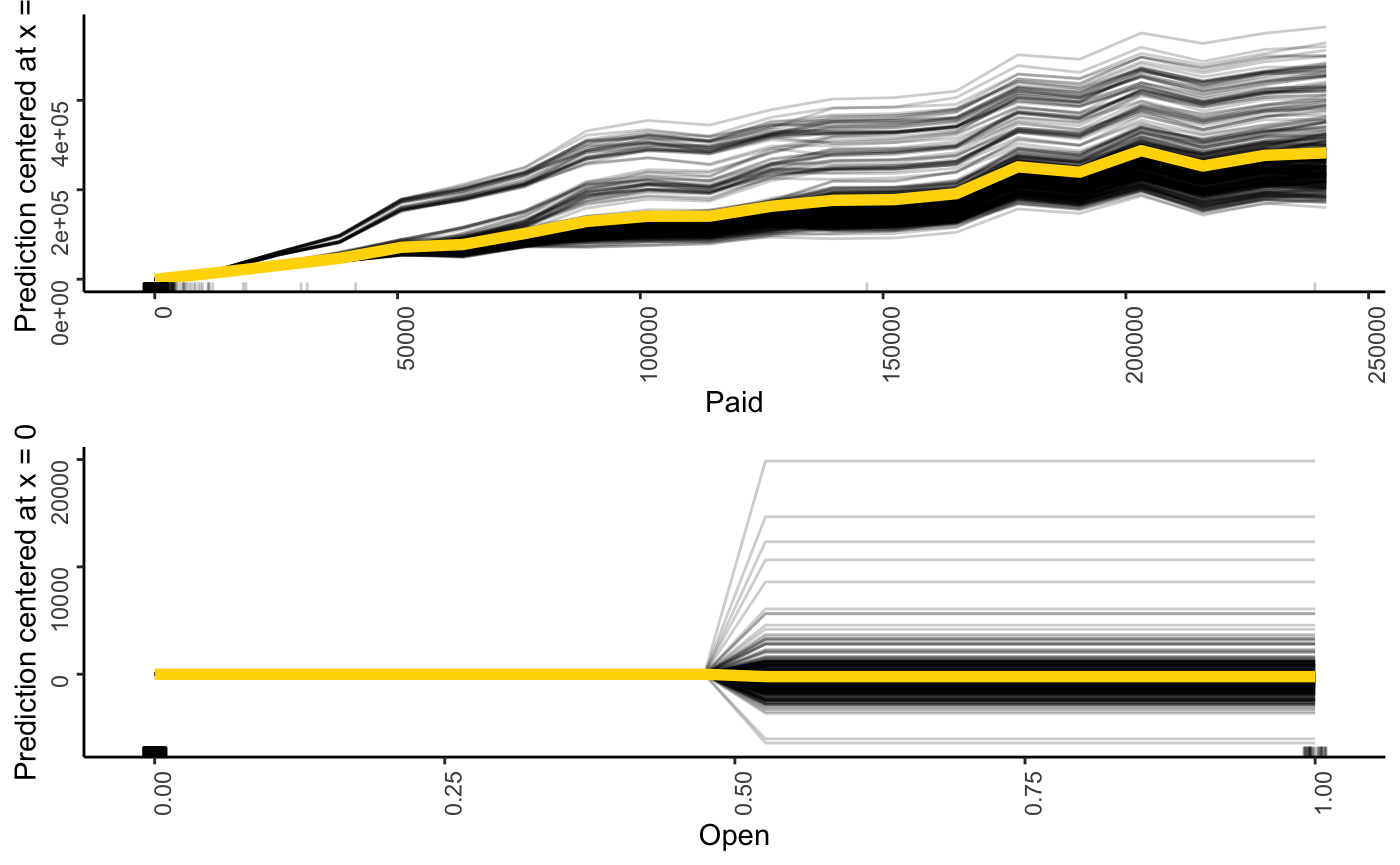
PDP/ICE plots

var2check <- c('Paid', 'Open')
pdp_ice <- lapply(var2check,
                 function(var){
                     FeatureEffect$new(predictor_a,
                                       feature = var,
                                       method = 'pdp+ice',
                                       center.at = 0) %>% 
                         plot() + theme_classic() + 
                         theme(axis.text = element_text(angle = 90, hjust = 1, vjust = 0.5))
                 })
# Produire les 4 graphiques dans une seule figure.
do.call('grid.arrange', pdp_ice)

Implémentation en R du modèle

Gabriel Crépeault-Cauchon

2019-12-21